2015-11-01

前回の話題のヒント

雑記

書いている時間がないのでヒントを

巡回セールスマン問題は対称群を引数に持つコスト関数の最小化問題とみなせる。
対称群は隣同士の互換から生成できる。

という事実をアニーリングに適用すると得られる。

ただし、スケーリングに関しての収束性のよさは不明。すこし調べた感じでは、誰もこの方法をやっていなかった*1。

改善方法としては、互換全体を元とするということも考えられる。収束が若干早くなる可能性がある。

もちろん巡回セールスマン問題は、この上なくよく考察されている問題の一つなので、ほかにもいろいろな解法や準解法がある。とくに、近似アルゴリズムは考えておくべき。

*1:やっぱり、スケーリングに対する収束速度が悪いのかな？

2015-10-12

ボルツマンマシンとはちょっと違うけど

雑記

bocchi-talks-information.hatenablog.com

をシミュレーティッドアニーリング的に（準）最適解を求める方法を少し考えたので、メモ的にソースコードだけでも。

解説はそのうちやります。

#define flp(i, n) for(int i = 0; i < n; ++i)
#include <iostream>
#include <bitset>
#include <cmath>
#include <iomanip>
#include <random>
using namespace std;

int main() {
    random_device rd;
    mt19937 mt(rd());
    uniform_real_distribution<double> score(0.0,1.0);
    
    
    int dist[7][7] = {
        {  0,124,127,125, 26, 54, 42},
        {124,  0, 77,165,116,143,150},
        {127, 77,  0,104,111,182,165},
        {125,165,104,  0,110,164,137},
        { 26,116,111,110,  0, 66, 65},
        { 54,143,182,164, 66,  0, 77},
        { 42,150,165,137, 65, 77,  0}
    };
    int minn = 10000;
    int prm[8], mprm[8];
    flp(k, 100){
        prm[0] = prm[7]  = 0;
        flp(i, 6) prm[i + 1] = i + 1;
        double T = 1000.0;
        flp(i, 200000){
            int j = i % 5 + 1;
            double dene = dist[ prm[j - 1] ][prm[j  + 1] ] - dist[ prm[j - 1] ][prm[j] ] +  dist[ prm[j] ][prm[j  + 2] ] - dist[ prm[j + 1] ][prm[j  + 2] ]; 
            double p = 1.0 / ( 1.0 + exp(  dene/T));
            double sc = score(mt);
            if(p > sc){int buf = prm[j]; prm[j] = prm[j + 1]; prm[j + 1] = buf;}
            if(i % 1000) T *= 0.9;
        }
        int sum = 0;
        flp(i, 7) sum += dist[ prm[i] ][prm[i  + 1] ];
        if( minn > sum) { flp(i, 8) mprm[i] = prm[i]; minn = sum;}
    }
    flp(i, 8) cout << mprm[i] << " "; cout << ": " << minn <<endl;
    return 0;
}

一応これでほとんど最適解にたどり着くはず。

2015-10-06

巡回セールスマン問題とボルツマンマシン

雑記

今回は、少し趣向を変えてボルツマンマシンが使われている例をみたいと思う。

参考にしたサイトは次のサイト。基本的にすべてここに書いてあることを焼きなおししようと思う。

ボルツマンマシンによる巡回セールスマン問題

ただし、今回は２５地点のリンクや重みを作るのが面倒だったため、関東地方の県庁所在地を車で移動した際にかかる距離で話を進めたいと思う。

問題設定

まずは関東地方の地図を見てもらいたい。世界地図

世界地図・日本地図の白地図を無料ダウンロード！【世界地図｜SEKAICHIZU】

という白地図を提供していただけるサイトを参考にすると、関東地方は

f:id:bottik:20151006160553g:plain

となっている。googleによると、これらの都市間の車での移動距離は単位をkmとして、

	水戸	宇都宮	前橋	さいたま	千葉	東京	横浜
水戸	0	77	165	116	143	124	150
宇都宮	77	0	104	111	182	127	165
前橋	165	104	0	110	164	125	137
さいたま	116	111	110	0	66	26	65
千葉	143	182	164	66	0	54	77
東京	124	127	125	26	54	0	42
横浜	150	165	137	65	77	42	0

らしい*1。

これらの都市を東京から出発して一回ずつまわり、最後に東京に戻ってくるその経路の中で最短なものはどれかと言う問題を考えよう。例のサイトにならって、

都市を表す変数を $X$ 、今何番目の都市かというのを表す変数を $i$ として、 $i$ 番目に $X$ にいるという変数を

${ \displaystyle x_{X,i}\in\{0,1\} }$

で表すとしよう。この変数が1であるならば $i$ 番目に $X$ にいるということになる。

さて、都市名をそのまま扱うのは少し煩雑なので、

	水戸	宇都宮	前橋	さいたま	千葉	東京	横浜
番号	1	2	3	4	5	0	6

と番号付けしておく。ここで、最初と最後が東京(番号0）なので、

${ \displaystyle x_{0,0} = x_{0,7} = 1 }$

${ \displaystyle x_{X,0} = x_{X,7} = 0,\ \ (X \neq 0) }$

がいえる。

また、同時に二つの都市に行かないだとか、同じ都市に2度行かないと言う条件は、

${ \displaystyle \sum_{i = 1}^6 x_{X,i} = 1,\ \ \sum_{X = 1}^6 x_{X,i} = 1 }$

となり、ある1つの経路の距離は、XとYとの距離を $d_{X,Y}$ とすれば、

${ \displaystyle \sum_{i = 1}^6\sum_{X =1}^6\sum_{Y \neq X}d_{X,Y}x_{X,i}(x_{Y,i-1} + x_{Y,i+1}) }$

と表せる。結局エネルギー関数は十分に大きな実数 $A,B$ を用いて、

${ \displaystyle E(x|A,B,d) = A \sum_{i = 1}^6\left(\sum_{X = 1}^6x_{X,i} - 1\right)^2 + B \sum_{X = 1}^6\left(\sum_{i = 1}^6x_{X,i} - 1\right)^2 + \sum_{i = 1}^6\sum_{X =1}^6\sum_{Y \neq X}d_{X,Y}x_{X,i}(x_{Y,i-1} + x_{Y,i+1}) }$

と表される。また、 $x_{X,i}^2 = x_{X,i}$ に注意して、エネルギーの定数項は無視できることを考えると、

${ \displaystyle E(x|A,B,d) = - (A + B) \sum_{i = 1}^6\sum_{X = 1}^6x_{X,i}+ 2A\sum_{i = 1}^6\sum_{X = 1}^6\sum_{Y \neq X}x_{X,i}x_{Y,i} + 2B\sum_{X = 1}^6\sum_{i = 1}^6\sum_{j \neq i}x_{X,i}x_{X,j}+ \sum_{i = 1}^6\sum_{X =1}^6\sum_{Y \neq X}d_{X,Y}x_{X,i}(x_{Y,i-1} + x_{Y,i+1}) }$

と表せる。なお、Gibbs samplingに用いる平均場エネルギーは

${ \displaystyle E(X,i|A,B,d) = - (A + B) + 2A\sum_{Y \neq X}x_{Y,i} + 2B\sum_{j \neq i}x_{X,j}+ \sum_{Y \neq X}d_{X,Y}(x_{Y,i-1} + x_{Y,i+1}) }$

となっている。

シミュレーティッド・アニーリング

今回は計算論的焼きなまし法とも言われる方法を用いて、最適解を確率的に計算する。

焼きなまし法（アニーリング）は物性分野（半導体物性とか）でも使われる言葉で、高温で焼いた金属や半導体などをゆっくりと冷やしていくことできれいな結晶を得ると言うものだ*2。

ともかく、シミュレーティッド・アニーリングには温度と言う要素が必要不可欠になる。具体的には、温度 $T$ を導入して、ギブスサンプリング的なことを行うのがシミュレーティッド・アニーリングになる。

つまり、

${ \displaystyle {\rm Pr}(x_{X,i} = 0 |A,B,d, T) = \frac{1}{1 + {\rm exp}(- E(X,i|A,B,d) /T)} }$

を用いて徐々に温度 $T$ を下げながら*3ユニットを更新していき、最終的な値を得ると言う方法だ。

計算してみる

今回もIdeoneに登場してもらって計算してみようと思う。

ideone.com

今回は都市数が少ないので事前に答えを求めておくことができる。次のC++14のコード

#include <iostream>
#include <algorithm>       
#include <vector>
#include <random>
using namespace std;

int main() {
    const int N = 6;
    int dist[7][7] = {
        {  0,124,127,125, 26, 54, 42},
        {124,  0, 77,165,116,143,150},
        {127, 77,  0,104,111,182,165},
        {125,165,104,  0,110,164,137},
        { 26,116,111,110,  0, 66, 65},
        { 54,143,182,164, 66,  0, 77},
        { 42,150,165,137, 65, 77,  0}
    };
    int min = 10000;
    vector<int> v(N), minv(N);
    iota(v.begin(), v.end(), 1);       
    do {
        int lsum = 0;
        int i = 0;
        for(i = 0; i < 6; ++i ){
            if(i == 0){lsum = dist[0][v[i]];}
            else{lsum += dist[v[i -1]][v[i]];}
            if(lsum > min)break;
        }
        if(lsum + dist[v[i-1]][0] < min){
            min = lsum + dist[v[i-1]][0];
            minv = v;
        }
    } while( next_permutation(v.begin(), v.end()) );  
    cout << min << endl;
    for(auto x : minv) cout << x << " "; cout << "\n";
    return 0;
}

に従うと0→4→3→2→1→5→6→0で579kmつまり

東京→さいたま→前橋→宇都宮→水戸→千葉→横浜→東京で579kmが最短だと言うのが分かる。

f:id:bottik:20151006184936j:plain

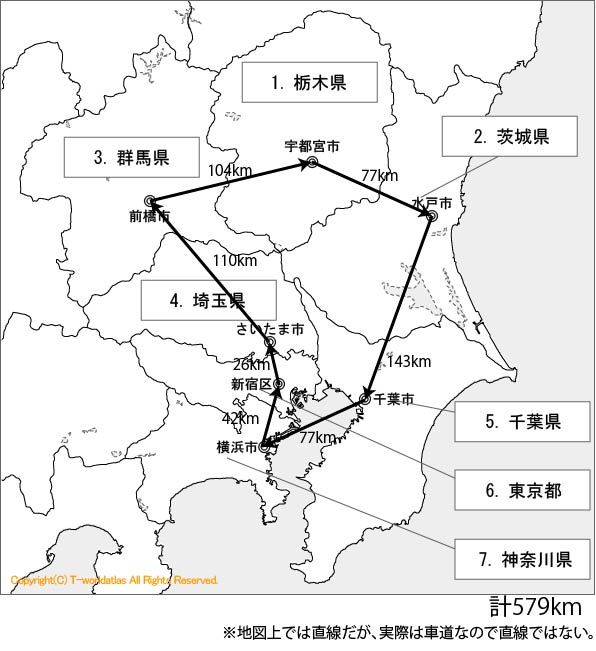
シミュレーティッド・アニーリングによる計算

ここで、 $A = B = 45$ としておく。

次のコードで挑戦してみるが、いまいち駄目。ミニマムに落ちるようにロールバックするという対策もあるけど、どうなんだろう。もう少しトライが必要みたい。

#include <iostream>
#include <bitset>
#include <cmath>
#include <iomanip>
#include <random>
using namespace std;

int main() {
    random_device rd;
    mt19937 mt(rd());
    uniform_real_distribution<double> score(0.0,1.0);
    
    double T = 100.0;
    int dist[7][7] = {
        {  0,124,127,125, 26, 54, 42},
        {124,  0, 77,165,116,143,150},
        {127, 77,  0,104,111,182,165},
        {125,165,104,  0,110,164,137},
        { 26,116,111,110,  0, 66, 65},
        { 54,143,182,164, 66,  0, 77},
        { 42,150,165,137, 65, 77,  0}
    };
    double p_ene[7][8];
    bool g_sample[7][8] = {0};
    g_sample[0][0] = true;
    g_sample[0][7] = true;
    double ene = 0;
    double pre_ene = 0;
    for(int j = 1; j < 7; ++j){
        for(int k = 1; k < 7; ++k){
            g_sample[j][k] = true;
        }
    }
    int g_sample_num = 4000000;
    for(int i = 0; i <  g_sample_num; ++i){
        for(int j = 1; j < 7; ++j){
            for(int k = 1; k < 7; ++k){
                int psum = 0;
                for(int l = 1; l < 7; ++l){
                    if(l != j) psum += g_sample[l][k];
                    if(l != k) psum += g_sample[j][l];
                }
                p_ene[j][k] = 90*( 1 - psum);
                psum = 0;
                for(int l = 1; l < 7; ++l){
                    if(l != j) psum -= dist[l][j] * (g_sample[l][k-1] + g_sample[l][k+1]);
                }
                p_ene[j][k] += psum;
            }
        }
        int j_site = (i % 36) % 6 + 1, k_site = (i % 36) / 6 + 1;
        double p = 1.0 / ( 1.0 + exp(p_ene[j_site][k_site])/T);
        double sc = score(mt);
        g_sample[j_site][k_site] = (sc > p);
        if(i % 15000 == 0){
            pre_ene = ene;
            ene = 0;
            for(int j = 1; j < 7; ++j){
                for(int k = 1; k < 7; ++k){
                    for(int l = 1; l < 7; ++l){
                        if(l != j) ene += dist[l][j] *g_sample[j][k] * (g_sample[l][k-1] + g_sample[l][k+1]);
                    }
                }
            }
            int prev = 0;
            int sumd = 0;
            for(int k = 1; k < 7; ++k){
                for(int j = 1; j < 7; ++j){
                    if(g_sample[j][k]) {
                        //cout << j << " "; 
                        sumd += dist[prev][j];
                        prev = j;
                    }
                }
            }
            sumd += dist[prev][0];
            //cout << sumd << endl;
            if(ene == pre_ene) T *= 0.95;    
        }
        
    }
    int prev = 0;
    int sumd = 0;
    for(int k = 1; k < 7; ++k){
            for(int j = 1; j < 7; ++j){
                if(g_sample[j][k]) {
                    cout << j << " "; 
                    sumd += dist[prev][j];
                    prev = j;
                }
            }
    }
    cout << endl;
    sumd += dist[prev][0];
    cout << sumd << endl;
    cout << T << endl;
    return 0;
}

1時間トライしても駄目。現時点での戒めもかねて公開。

*1:実際は出発点と到着点が逆転すると使用する道が異なって距離が変わるのだけれど、簡単のため対称にしてある。

*2:真空分野でも使われるけど、また違った意味、水を飛ばして真空度を上げるときに使われる。

*3:実用上はこの温度の下げ方がかなり重要な要素となる。急に冷えすぎると局所最適解から出られなくなり、冷やし方が遅すぎると計算が終わらない。

2015-10-06

Gibbs sampling について

ボルツマンマシン講座

ボルツマンマシンの状態数

前回はなしたボルツマンマシンだけれど、実際に学習を実行しようとなると、あるパラメータにおける期待値を計算する必要がある。期待値は例えば、

${ \displaystyle E[X_i X_j] = \sum_{x\in\mathcal{X}}p(x)x_ix_j }$

というようなもので、ボルツマンマシンは $\{ 0,1\}^n$ 上の確率分布だったから、 $n$ が大きくなると足す必要のある数は爆発的に大きくなる。要するに、実際の計算機ではやっていられなくなる。そこでちょっとした工夫が必要になる。

全結合ボルツマンマシンの例

今回は次のボルツマンマシンを使う。 $n = 4$

${ \displaystyle b = ( 1, -3.5, -1, 2) }$

$w =$


0	-2	-1	3
-2	0	-1	2
-1	-1	0	2
3	2	2	0

このボルツマンマシンの分布は次のようになる。

状態	確率（％）
0000	0.06
0001	0.16
0010	0.00
0011	0.03
0100	0.02
0101	0.02
0110	0.00
0111	0.00
1000	0.42
1001	23.02
1010	0.09
1011	37.95
1100	1.15
1101	23.02
1110	0.09
1111	13.96

ちなみにこの分布を求めて、そこからサンプリングして経験分布を得るC++14のコードは次のようになる*1。

#include <iostream>
#include <bitset>
#include <cmath>
#include <iomanip>
#include <random>
using namespace std;

int main() {
    random_device rd;
    mt19937 mt(rd());
    uniform_real_distribution<double> score(0.0,1.0);
    
    double energy[16] = {0};
    double e_ene[16] = {0};
    double prob[16];
    double i_prob[16] = {0};
    double t_e_ene = 0;
    double b[4] = {1,-3.5,-1,2};
    double w[4][4] = {
        { 0, 2,-1, 3},
        { 2, 0,-1, 2},
        {-1,-1, 0, 2},
        { 3, 2, 2, 0}
    };
    
    for(int i = 0; i < 16; ++i){
        bitset<4> sample(i);
        for(int j = 0; j < 4; ++j){
            energy[i] -= sample[j] * b[j];
            for(int k = j + 1; k < 4; ++k){
                energy[i] -= sample[j] * sample[k] *w[j][k];
            }
        }
        e_ene[i] = exp( -energy[i] );
        t_e_ene += e_ene[i];
    }
    for(int i = 0; i < 16; ++i){
        prob[i] = e_ene[i] / t_e_ene;
        if( i ) {i_prob[i] = i_prob[i-1] +  prob[i];}
        else{i_prob[i] =  prob[i];}
    }
    
    int n_count[16] = {0};
    int sample_num = 1000000;
    for(int j = 0; j < sample_num; ++j){
        double sc = score(mt);
        for(int i = 0; i < 16; ++i){
            if(i_prob[i] > sc){
                n_count[i]++ ;
                break;
            }
        }
    }
    
    for(int i = 0; i < 16; ++i){
        cout << static_cast< bitset<4> >(i) << fixed << setprecision(2)<<" " << (double) 100 * n_count[i] / sample_num <<" " << prob[i] * 100 <<  endl;
    }
    return 0;
}

Gibbs sampling

このサンプリング法では、すべての状態についての確率を求めていた*2。しかし、 $n$ が増えれば増えるほど、このやり方は無理になっていく。

ここで、ボルツマンマシンの構造からギブスサンプリングを用いることを考える。

ギブスサンプリングとは、ある状態のあるユニットに注目し、他のユニットの値は定まっているものとして、その注目しているユニットの値を更新していく方法で、十分長い間この更新を繰り返すと所望の分布から生成されたサンプルが得られると理論的には保証されている方法だ。

あるユニット $x_i$ に注目したときに、他のユニットの値が定まっているときのユニット $x_i$ の分布は、

${ \displaystyle {\rm Pr}(X_i = 0|b,w,\{x_j\}_{j \neq i}) = \frac{1}{ 1 + {\rm exp}(b_i + \sum_{j \neq i}w_{i,j}x_j)} }$

で定まる。

この分布を用いてサンプルを行い、もとの分布と比較するコードを次に紹介する。

#include <iostream>
#include <bitset>
#include <cmath>
#include <iomanip>
#include <random>
using namespace std;

int main() {
    random_device rd;
    mt19937 mt(rd());
    uniform_real_distribution<double> score(0.0,1.0);
    
    double energy[16] = {0};
    double e_ene[16] = {0};
    double prob[16];
    double i_prob[16] = {0};
    double t_e_ene = 0;
    double b[4] = {1,-3.5,-1,2};
    double w[4][4] = {
        { 0, 2,-1, 3},
        { 2, 0,-1, 2},
        {-1,-1, 0, 2},
        { 3, 2, 2, 0}
    };
    double p_ene[4];
    bitset<4> g_sample (0);

    int g_n_count[16] = {0};
    int g_sample_num = 1000000;
    int g_s_t = 0;
    for(int i = 0; i <  g_sample_num; ++i){
        for(int j = 0; j < 4; ++j){
            p_ene[j] = b[j];
            for(int k = 0; k < 4; ++k){
                if(k != j)    p_ene[j] += w[k][j] * g_sample[k];
            }
        }
        int i_site = i % 4;
        double p = 1.0 / ( 1.0 + exp(p_ene[i_site]));
        double sc = score(mt);
        g_sample[i_site] = (sc > p);
        if((i > g_sample_num / 10) && (i % 51 == 0) ){
            int nnn = g_sample.to_ulong();
            g_n_count[nnn]++;
            g_s_t++;
        }
    }
    
    for(int i = 0; i < 16; ++i){
        bitset<4> sample(i);
        for(int j = 0; j < 4; ++j){
            energy[i] -= sample[j] * b[j];
            for(int k = j + 1; k < 4; ++k){
                energy[i] -= sample[j] * sample[k] *w[j][k];
            }
        }
        e_ene[i] = exp( -energy[i] );
        t_e_ene += e_ene[i];
    }
    for(int i = 0; i < 16; ++i){
        prob[i] = e_ene[i] / t_e_ene;
        if( i ) {i_prob[i] = i_prob[i-1] +  prob[i];}
        else{i_prob[i] =  prob[i];}
    }
    for(int i = 0; i < 16; ++i){
        cout << static_cast< bitset<4> >(i) << fixed << setprecision(2)<<" " << (double) 100 * g_n_count[i] / g_s_t <<" " << prob[i] * 100 <<  endl;
    }
    return 0;
}

このコードでは状態を0000から始めて、更新回数の10分の1をburn-in期間において51回の更新毎にサンプリングしてある。結果の一例を次に書く*3。

状態	Gibbs samplingによる経験分布の確率（％）	計算による真の確率（％）
0000	0.06	0.06
0001	0.17	0.16
0010	0.00	0.00
0011	0.02	0.03
0100	0.03	0.02
0101	0.02	0.02
0110	0.00	0.00
0111	0.00	0.00
1000	0.37	0.42
1001	23.06	23.02
1010	0.14	0.09
1011	37.85	37.95
1100	1.14	1.15
1101	23.43	23.02
1110	0.07	0.09
1111	13.65	13.96

サンプル数が少ないかもしれないが、まずまず良い結果を得られていると思われる。

このギブスサンプリングを用いてあるパラメータにおける期待値を近似的に求めることができる。これが、ボルツマンマシンの学習に重要となってくる。

どう重要になってくるかは、後日書こうと思う。

*1:コードは初心者なので汚いのは許してください。

*2:もちろんサンプルするために確率を求めるのはナンセンスであって、本来は確率から得られる期待値などを計算する為にサンプルする

*3:codeはideone

ideone.com

で動作することは確認済み

2015-10-02

ボルツマンマシンとは

ボルツマンマシン講座

本の紹介

基本的には、

深層学習 (機械学習プロフェッショナルシリーズ)

作者: 岡谷貴之
出版社/メーカー: 講談社
発売日: 2015/04/08
メディア: 単行本（ソフトカバー）
この商品を含むブログ (6件) を見る

の最終章をいろいろと端折りながら紹介する。

ボルツマンマシンの状態

すごく大雑把に言えば、ボルツマンマシンとは指数型分布族の一種のこと。下の絵の様な構造を持っている。

f:id:bottik:20151002181527j:plain

ここで、丸はユニットとよばれ、それぞれ0か1の値をとり、ユニットの全体が確率変数となる。つまりユニットが $n$ 個あった場合、そのボルツマンマシンは $\{ 0,1\}^n$ 上の確率分布になっている。上の絵の場合はユニットが10個あるので、とりうる値としては0000000000から1111111111までの1024個あることになる。

ここで、このとる値のことを状態と呼ぶことにして、 $x$ で表すことにする。つまり絵の場合は、 $x \in \{ 0,1\}^{10}$ だ。

また、 $i$ 番目のユニットがとる値を $x_i\in \{ 0,1\}$ で表すことにする。

エネルギーと確率

ユニットが $n$ 個あった場合、そのボルツマンマシンは $\{ 0,1\}^n$ 上の確率分布になっている。と書いたが、その分布は具体的にどう決めるのだろうか？

物理ではよく「エネルギーが低いと安定する」と言われるけれど、その概念を持ち出してくる。「安定する」というのを、「確率が高い」と読み替える。とにかく、ボルツマンマシンの確率分布はエネルギーを用いて定義する。

ここで、エネルギー関数 $E : \{ 0,1\}^n \to \mathbb{R}_+$ を考える。これは、状態が決まればエネルギーの大きさが決まる関数のこと。今は物理をやっているわけではないのでエネルギーの単位は考えない。大きさだけ分かればいい。

このエネルギーに応じて、ある状態 $x$ にある確率 $p(x)$ が

${ \displaystyle p(x) \propto {\rm exp}(-E(x)) }$

であるとする。つまり、

${ \displaystyle p(x) = \frac{{\rm exp}(-E(x))}{\sum_{x'}{\rm exp}(-E(x'))} }$

であるとする。この確率分布はBoltzmann分布と呼ばれて*1、統計力学でよく目にする。

見てのとおり、エネルギーが大きいと確率が低いと言うのが分かる。

エネルギー関数と指数型分布族

上で書いたとおり、ある状態がボルツマン分布に従うならば、エネルギー関数を決めれば確率が求まると言うことが分かる。

ところで、指数型分布族は、

${ \displaystyle \log p(x|\theta) = C(x) + \sum_{i = 1}^k \theta^i F_i(x) - \psi(\theta) }$

と言う形をしていた。もしエネルギー関数がパラメータ $\theta$ に対して、

${ \displaystyle -E(x|\theta) = C(x) + \sum_{i = 1}^k \theta^i F_i(x) }$

と言う形をしているならば、ボルツマン分布は指数型分布族（の元）になっている。

ボルツマンマシンの確率分布

ここで、各ユニット $i$ とユニット間 $(i,j)$ に対して実数パラメータ $b_i$ と $w_{i,j}$ を導入しよう。これらを使ってエネルギー関数が、

${ \displaystyle -E(x|b,w) = \sum_{i = 1}^n b_i x_i + \sum_{i > j} w_{i,j}x_ix_j }$

とかけている場合、これは実数パラメータ $b_i$ と $w_{i,j}$ に関する指数型分布族になっている。

ボルツマンマシンは、この確率分布に従う。

基本的なボルツマンマシンの使用方法は、次のとおり。

学習データからラベルに対応した実数パラメータ $b_i$ と $w_{i,j}$ を学習する。
サンプルがどのラベルに対応しているかを検定する。（＝サンプルにラベル付けを行う。）

検定の方法については、ちょっと前に書いた

bocchi-talks-information.hatenablog.com

の方法を少し工夫するとできるのだけれども、学習データからラベルに対応した実数パラメータ $b_i$ と $w_{i,j}$ を学習するのは、結構骨が折れる。次回はこのボルツマンマシンの学習について書きたいと思う。

*1:Gibbs分布とも、Gibbs=Boltzmann分布とも呼ばれる。

2015-09-25

準備中

雑記

学会予稿やら、博士論文の最終稿やらでここ数日ネタを考えてませんでした。

そしたら、その間に

itpro.nikkeibp.co.jp

内容そのものは

www.nature.com

と言う話がhotになってきたので、次回から少し脱線して

ボルツマンマシンや、ディープラーニング、最終的にこの稿のダイナミックボルツマンマシンの解説でもしようと考え中。

乞うご期待。

2015-09-20

不偏推定量について

初歩からの検定・推定理論講座

今日は、推定理論にもどって、不偏推定量について書こうと思う。

設定

データ集合 $\mathcal{X}$ が与えられているとして、 $\mathcal{P(X)}$ を集合 $\mathcal{X}$ 上の確率分布全体のなす集合とする。また、モデルとして、 $M = \{ p(x|\theta) \in \mathcal{P(X)}| \theta \in \Theta \subset \mathbb{R}^k \}$ を仮定する。

同時独立分布

今回も、データが出てくる順番に関係なく毎回モデル $M$ 上の分布 $p^*\in M$ にしたがって出てくるとする。つまり、データ列が確率変数 $X^N = (X^{(1)}X^{(2)}\cdots X^{(N)})$ であり、各 $j$ について $X^{(j)}$ が確率分布 $p^*(x) \in M \subset \mathcal{P(X)}$ に従っているとする。このとき、データ列の具体値 $x^N = (x^{(1)}x^{(2)}\cdots x^{(N)})$ が得られる確率は