巡回セールスマン問題とボルツマンマシン - 情報理論関連をぐだぐだと

今回は、少し趣向を変えてボルツマンマシンが使われている例をみたいと思う。

参考にしたサイトは次のサイト。基本的にすべてここに書いてあることを焼きなおししようと思う。

ボルツマンマシンによる巡回セールスマン問題

ただし、今回は２５地点のリンクや重みを作るのが面倒だったため、関東地方の県庁所在地を車で移動した際にかかる距離で話を進めたいと思う。

問題設定

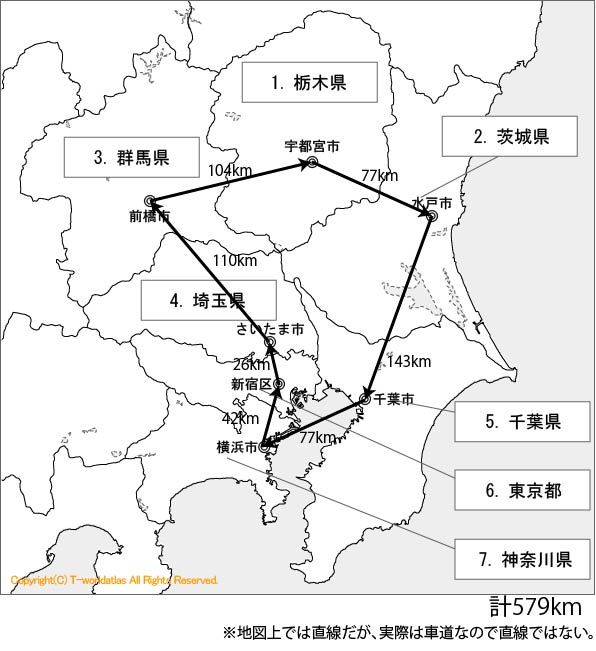
まずは関東地方の地図を見てもらいたい。世界地図

世界地図・日本地図の白地図を無料ダウンロード！【世界地図｜SEKAICHIZU】

という白地図を提供していただけるサイトを参考にすると、関東地方は

f:id:bottik:20151006160553g:plain

となっている。googleによると、これらの都市間の車での移動距離は単位をkmとして、

	水戸	宇都宮	前橋	さいたま	千葉	東京	横浜
水戸	0	77	165	116	143	124	150
宇都宮	77	0	104	111	182	127	165
前橋	165	104	0	110	164	125	137
さいたま	116	111	110	0	66	26	65
千葉	143	182	164	66	0	54	77
東京	124	127	125	26	54	0	42
横浜	150	165	137	65	77	42	0

らしい*1。

これらの都市を東京から出発して一回ずつまわり、最後に東京に戻ってくるその経路の中で最短なものはどれかと言う問題を考えよう。例のサイトにならって、

都市を表す変数を $X$ 、今何番目の都市かというのを表す変数を $i$ として、 $i$ 番目に $X$ にいるという変数を

${ \displaystyle x_{X,i}\in\{0,1\} }$

で表すとしよう。この変数が1であるならば $i$ 番目に $X$ にいるということになる。

さて、都市名をそのまま扱うのは少し煩雑なので、

	水戸	宇都宮	前橋	さいたま	千葉	東京	横浜
番号	1	2	3	4	5	0	6

と番号付けしておく。ここで、最初と最後が東京(番号0）なので、

${ \displaystyle x_{0,0} = x_{0,7} = 1 }$

${ \displaystyle x_{X,0} = x_{X,7} = 0,\ \ (X \neq 0) }$

がいえる。

また、同時に二つの都市に行かないだとか、同じ都市に2度行かないと言う条件は、

${ \displaystyle \sum_{i = 1}^6 x_{X,i} = 1,\ \ \sum_{X = 1}^6 x_{X,i} = 1 }$

となり、ある1つの経路の距離は、XとYとの距離を $d_{X,Y}$ とすれば、

${ \displaystyle \sum_{i = 1}^6\sum_{X =1}^6\sum_{Y \neq X}d_{X,Y}x_{X,i}(x_{Y,i-1} + x_{Y,i+1}) }$

と表せる。結局エネルギー関数は十分に大きな実数 $A,B$ を用いて、

${ \displaystyle E(x|A,B,d) = A \sum_{i = 1}^6\left(\sum_{X = 1}^6x_{X,i} - 1\right)^2 + B \sum_{X = 1}^6\left(\sum_{i = 1}^6x_{X,i} - 1\right)^2 + \sum_{i = 1}^6\sum_{X =1}^6\sum_{Y \neq X}d_{X,Y}x_{X,i}(x_{Y,i-1} + x_{Y,i+1}) }$

と表される。また、 $x_{X,i}^2 = x_{X,i}$ に注意して、エネルギーの定数項は無視できることを考えると、

${ \displaystyle E(x|A,B,d) = - (A + B) \sum_{i = 1}^6\sum_{X = 1}^6x_{X,i}+ 2A\sum_{i = 1}^6\sum_{X = 1}^6\sum_{Y \neq X}x_{X,i}x_{Y,i} + 2B\sum_{X = 1}^6\sum_{i = 1}^6\sum_{j \neq i}x_{X,i}x_{X,j}+ \sum_{i = 1}^6\sum_{X =1}^6\sum_{Y \neq X}d_{X,Y}x_{X,i}(x_{Y,i-1} + x_{Y,i+1}) }$

と表せる。なお、Gibbs samplingに用いる平均場エネルギーは

${ \displaystyle E(X,i|A,B,d) = - (A + B) + 2A\sum_{Y \neq X}x_{Y,i} + 2B\sum_{j \neq i}x_{X,j}+ \sum_{Y \neq X}d_{X,Y}(x_{Y,i-1} + x_{Y,i+1}) }$

となっている。

シミュレーティッド・アニーリング

今回は計算論的焼きなまし法とも言われる方法を用いて、最適解を確率的に計算する。

焼きなまし法（アニーリング）は物性分野（半導体物性とか）でも使われる言葉で、高温で焼いた金属や半導体などをゆっくりと冷やしていくことできれいな結晶を得ると言うものだ*2。

ともかく、シミュレーティッド・アニーリングには温度と言う要素が必要不可欠になる。具体的には、温度 $T$ を導入して、ギブスサンプリング的なことを行うのがシミュレーティッド・アニーリングになる。

つまり、

${ \displaystyle {\rm Pr}(x_{X,i} = 0 |A,B,d, T) = \frac{1}{1 + {\rm exp}(- E(X,i|A,B,d) /T)} }$

を用いて徐々に温度 $T$ を下げながら*3ユニットを更新していき、最終的な値を得ると言う方法だ。

計算してみる

今回もIdeoneに登場してもらって計算してみようと思う。

ideone.com

今回は都市数が少ないので事前に答えを求めておくことができる。次のC++14のコード

#include <iostream>
#include <algorithm>       
#include <vector>
#include <random>
using namespace std;

int main() {
    const int N = 6;
    int dist[7][7] = {
        {  0,124,127,125, 26, 54, 42},
        {124,  0, 77,165,116,143,150},
        {127, 77,  0,104,111,182,165},
        {125,165,104,  0,110,164,137},
        { 26,116,111,110,  0, 66, 65},
        { 54,143,182,164, 66,  0, 77},
        { 42,150,165,137, 65, 77,  0}
    };
    int min = 10000;
    vector<int> v(N), minv(N);
    iota(v.begin(), v.end(), 1);       
    do {
        int lsum = 0;
        int i = 0;
        for(i = 0; i < 6; ++i ){
            if(i == 0){lsum = dist[0][v[i]];}
            else{lsum += dist[v[i -1]][v[i]];}
            if(lsum > min)break;
        }
        if(lsum + dist[v[i-1]][0] < min){
            min = lsum + dist[v[i-1]][0];
            minv = v;
        }
    } while( next_permutation(v.begin(), v.end()) );  
    cout << min << endl;
    for(auto x : minv) cout << x << " "; cout << "\n";
    return 0;
}

に従うと0→4→3→2→1→5→6→0で579kmつまり

東京→さいたま→前橋→宇都宮→水戸→千葉→横浜→東京で579kmが最短だと言うのが分かる。

f:id:bottik:20151006184936j:plain

シミュレーティッド・アニーリングによる計算

ここで、 $A = B = 45$ としておく。

次のコードで挑戦してみるが、いまいち駄目。ミニマムに落ちるようにロールバックするという対策もあるけど、どうなんだろう。もう少しトライが必要みたい。

#include <iostream>
#include <bitset>
#include <cmath>
#include <iomanip>
#include <random>
using namespace std;

int main() {
    random_device rd;
    mt19937 mt(rd());
    uniform_real_distribution<double> score(0.0,1.0);
    
    double T = 100.0;
    int dist[7][7] = {
        {  0,124,127,125, 26, 54, 42},
        {124,  0, 77,165,116,143,150},
        {127, 77,  0,104,111,182,165},
        {125,165,104,  0,110,164,137},
        { 26,116,111,110,  0, 66, 65},
        { 54,143,182,164, 66,  0, 77},
        { 42,150,165,137, 65, 77,  0}
    };
    double p_ene[7][8];
    bool g_sample[7][8] = {0};
    g_sample[0][0] = true;
    g_sample[0][7] = true;
    double ene = 0;
    double pre_ene = 0;
    for(int j = 1; j < 7; ++j){
        for(int k = 1; k < 7; ++k){
            g_sample[j][k] = true;
        }
    }
    int g_sample_num = 4000000;
    for(int i = 0; i <  g_sample_num; ++i){
        for(int j = 1; j < 7; ++j){
            for(int k = 1; k < 7; ++k){
                int psum = 0;
                for(int l = 1; l < 7; ++l){
                    if(l != j) psum += g_sample[l][k];
                    if(l != k) psum += g_sample[j][l];
                }
                p_ene[j][k] = 90*( 1 - psum);
                psum = 0;
                for(int l = 1; l < 7; ++l){
                    if(l != j) psum -= dist[l][j] * (g_sample[l][k-1] + g_sample[l][k+1]);
                }
                p_ene[j][k] += psum;
            }
        }
        int j_site = (i % 36) % 6 + 1, k_site = (i % 36) / 6 + 1;
        double p = 1.0 / ( 1.0 + exp(p_ene[j_site][k_site])/T);
        double sc = score(mt);
        g_sample[j_site][k_site] = (sc > p);
        if(i % 15000 == 0){
            pre_ene = ene;
            ene = 0;
            for(int j = 1; j < 7; ++j){
                for(int k = 1; k < 7; ++k){
                    for(int l = 1; l < 7; ++l){
                        if(l != j) ene += dist[l][j] *g_sample[j][k] * (g_sample[l][k-1] + g_sample[l][k+1]);
                    }
                }
            }
            int prev = 0;
            int sumd = 0;
            for(int k = 1; k < 7; ++k){
                for(int j = 1; j < 7; ++j){
                    if(g_sample[j][k]) {
                        //cout << j << " "; 
                        sumd += dist[prev][j];
                        prev = j;
                    }
                }
            }
            sumd += dist[prev][0];
            //cout << sumd << endl;
            if(ene == pre_ene) T *= 0.95;    
        }
        
    }
    int prev = 0;
    int sumd = 0;
    for(int k = 1; k < 7; ++k){
            for(int j = 1; j < 7; ++j){
                if(g_sample[j][k]) {
                    cout << j << " "; 
                    sumd += dist[prev][j];
                    prev = j;
                }
            }
    }
    cout << endl;
    sumd += dist[prev][0];
    cout << sumd << endl;
    cout << T << endl;
    return 0;
}

1時間トライしても駄目。現時点での戒めもかねて公開。

*1:実際は出発点と到着点が逆転すると使用する道が異なって距離が変わるのだけれど、簡単のため対称にしてある。

*2:真空分野でも使われるけど、また違った意味、水を飛ばして真空度を上げるときに使われる。

*3:実用上はこの温度の下げ方がかなり重要な要素となる。急に冷えすぎると局所最適解から出られなくなり、冷やし方が遅すぎると計算が終わらない。